Merge Sort Algorithm

Problem:  Given an array of size n, sort the array using Merge Sort.

Examples:

Example 1:
Input: N=5, arr[]={4,2,1,6,7}
Output: 1,2,4,6,7,


Example 2:
Input: N=7,arr[]={3,2,8,5,1,4,23}
Output: 1,2,3,4,5,8,23

Solution

Disclaimer: Don’t jump directly to the solution, try it out yourself first.

Solution : 

Intuition: 

1. Merge Sort is a divide and conquers algorithm, it divides the given array into equal parts and then merges the 2 sorted parts. 
2. There are 2 main functions :
   merge(): This function is used to merge the 2 halves of the array. It assumes that both parts of the array are sorted and merges both of them.
   mergeSort(): This function divides the array into 2 parts. low to mid and mid+1 to high where,

 low = leftmost index of the array
 high = rightmost index of the array
 mid = Middle index of the array 

3. We recursively split the array, and go from top-down until all sub-arrays size becomes 1.

Approach : 

Approach:

• We will be creating 2 functions mergeSort() and merge().
• mergeSort(arr[], low, high):
  1. In order to implement merge sort we need to first divide the given array into two halves. Now, if we carefully observe, we need not divide the array and create a separate array, but we will divide the array’s range into halves every time. For example, the given range of the array is 0 to 4(0-based indexing). Now on the first go, we will divide the range into half like (0+4)/2 = 2. So, the range of the left half will be 0 to 2 and for the right half, the range will be 3 to 4. Similarly, if the given range is low to high, the range for the two halves will be low to mid and mid+1 to high, where mid = (low+high)/2. This process will continue until the range size becomes.
     
  2. So, in mergeSort(), we will divide the array around the middle index(rather than creating a separate array) by making the recursive call :
     1. mergeSort(arr,low,mid)   [Left half of the array]
     2. mergeSort(arr,mid+1,high)  [Right half of the array]
     where low = leftmost index of the array, high = rightmost index of the array, and mid = middle index of the array.
  3. Now, in order to complete the recursive function, we need to write the base case as well. We know from step 2.1, that our recursion ends when the array has only 1 element left. So, the leftmost index, low, and the rightmost index high become the same as they are pointing to a single element.
     Base Case: if(low >= high) return;
• Pseudocode:

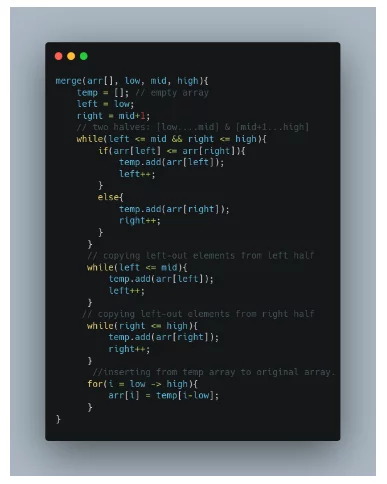
• merge(arr[], low, mid, high):
  1. In the merge function, we will use a temp array to store the elements of the two sorted arrays after merging. Here, the range of the left array is low to mid and the range for the right half is mid+1 to high.
  2. Now we will take two pointers left and right, where left starts from low and right starts from mid+1.
  3. Using a while loop( while(left <= mid && right <= high)), we will select two elements, one from each half, and will consider the smallest one among the two. Then, we will insert the smallest element in the temp array.
  4. After that, the left-out elements in both halves will be copied as it is into the temp array.
  5. Now, we will just transfer the elements of the temp array to the range low to high in the original array. The pseudo code will look like the following:

The red number shows the order of the steps in recursion calls.

Code:

• C++ Code
• Java Code

import java.util.*;

class Solution {
    private static void merge(int[] arr, int low, int mid, int high) {
        ArrayList<Integer> temp = new ArrayList<>(); // temporary array
        int left = low;      // starting index of left half of arr
        int right = mid + 1;   // starting index of right half of arr

        //storing elements in the temporary array in a sorted manner//

        while (left <= mid && right <= high) {
            if (arr[left] <= arr[right]) {
                temp.add(arr[left]);
                left++;
            } else {
                temp.add(arr[right]);
                right++;
            }
        }

        // if elements on the left half are still left //

        while (left <= mid) {
            temp.add(arr[left]);
            left++;
        }

        //  if elements on the right half are still left //
        while (right <= high) {
            temp.add(arr[right]);
            right++;
        }

        // transfering all elements from temporary to arr //
        for (int i = low; i <= high; i++) {
            arr[i] = temp.get(i - low);
        }
    }

    public static void mergeSort(int[] arr, int low, int high) {
        if (low >= high) return;
        int mid = (low + high) / 2 ;
        mergeSort(arr, low, mid);  // left half
        mergeSort(arr, mid + 1, high); // right half
        merge(arr, low, mid, high);  // merging sorted halves
    }
}
public class tUf {
    public static void main(String args[]) {
        Scanner sc = new Scanner(System.in);
        int n = 7;
        int arr[] = { 9, 4, 7, 6, 3, 1, 5 };
        System.out.println("Before sorting array: ");
        for (int i = 0; i < n; i++) {
            System.out.print(arr[i] + " ");
        }
        System.out.println();
        Solution.mergeSort(arr, 0, n - 1);
        System.out.println("After sorting array: ");
        for (int i = 0; i < n; i++) {
            System.out.print(arr[i] + " ");
        }
        System.out.println();
    }

}

Output:

Before Sorting Array:
9 4 7 6 3 1 5
After Sorting Array:
1 3 4 5 6 7 9

Time complexity: O(nlogn) 

Reason: At each step, we divide the whole array, for that logn and we assume n steps are taken to get a sorted array, so overall time complexity will be nlogn

Space complexity: O(n)  

Reason: We are using a temporary array to store elements in sorted order.

Auxiliary Space Complexity: O(n)